HOE DE LEVENSDUUR VAN EEN WENTELLAGER VERLENGEN?
een zeer acceptabele levensduur hebben wanneer er rekening wordt gehouden met onder meer een goede smering en het voorkomen van vervuiling
Het belang van goede smering
Een tijdje terug organiseerde FEDA, de Nederlandse branchevereniging voor aandrijf- en automatiseringstechniek, samen met de eveneens Nederlandse Vereniging Platform Hydrauliek, de tweejaarlijkse DFPTC: Dutch Fluid Power Transmission Conference. Bij deze editie werd de hydraulische aandrijftechniek gekoppeld aan 'grote aandrijvingen', een thema dat onder meer werd ingevuld met een lezing over de levensduurberekening van lagers. Van oudsher wordt hiervoor uitgegaan van het dynamische draaggetal van een lager dat wordt gedeeld door de belasting, waarna de constructeur dit resultaat verheft tot een lagerafhankelijke macht. Deze berekening blijkt echter niet optimaal betrouwbaar omdat factoren als smering, de verhouding tussen de belasting en vermoeiingsgrens en verontreinigingen een (meer dan) significante invloed hebben op de levensduur.
LEVENSDUUR BEPAALT DIMENSIONERING
De constructie en dimensionering van de verschillende componenten van een aandrijflijn zijn onder meer afhankelijk van de gewenste levensduur. Om te bepalen welke component het best past in een samenstelling, worden er zogenaamde levensduurberekeningen uitgevoerd. Hierin worden diverse grootheden betrokken die invloed hebben op de levensduur.
Kijken we naar een lager, dan is de levensduur te beschouwen als resultaat van de respectievelijke levensduur van de loopbanen, de wentellichamen, de kooi, het smeermiddel en de afdichting. Deze levensduur wordt negatief beïnvloed door enerzijds schade als gevolg van veranderingen die optreden aan het oppervlak van de loopvlakken, en anderzijds door schade als gevolg van veranderingen die eronder optreden. In het eerste geval gaat het om mechanische slijtage die grotendeels - of praktisch helemaal - te voorkomen is door goed met het juiste smeermiddel en bij voldoende zuiverheid te smeren. Wat zich ónder het oppervlak afspeelt, is gerelateerd aan vermoeiing van het materiaal en wordt bepaald door de hoogte en het type belasting. Hoewel deze schade niet zichtbaar is, speelt ze wel degelijk een belangrijke rol in het kader van de levensduur.
GESCHIEDENIS VAN LEVENSDUURBEREKENING LAGER
Omdat lagers al decennialang een belangrijke rol spelen in aandrijflijnen, is er al relatief vroeg (in de jaren 40 van de vorige eeuw door de Zweedse ingenieurs Gustav Lundberg en Arvid Palmgren) een basis gelegd voor de levensduurberekening van deze componenten. Het ging daarbij om een wiskundige basis die door de jaren heen verder werd verfijnd in relatie tot nieuw vergaarde kennis inzake materialen, productietechnieken en lagerontwerpen. In 1977 werd de basis gelegd voor de ISO 281-standaard uit 1990. Deze is gebaseerd op de aanname dat 90% van de lagers de berekende levensduur haalt, en is weergegeven in de hierop volgende formule. 
Bij de analyse van deze formule zien we dat de levensduur van een lager wordt berekend door het dynamische draaggetal van het lager te delen door de equivalente belasting en tot een macht te verheffen die afhankelijk is van het type lager. Het dynamische draaggetal C wordt uitgedrukt in newton en gebruikt voor berekeningen waarbij er een zekere belasting wordt uitgeoefend op roterende lagers. Deze waarde betreft de lagerbelasting die volgens ISO 281:1990 een levensduur van 1.000.000 omwentelingen oplevert. Daarbij wordt aangenomen dat de belasting constant van grootte en richting is, radiaal is voor radiale lagers en zuiver axiaal, dus centraal werkend, voor axiale lagers.
KWALITEITSVERGELIJKING
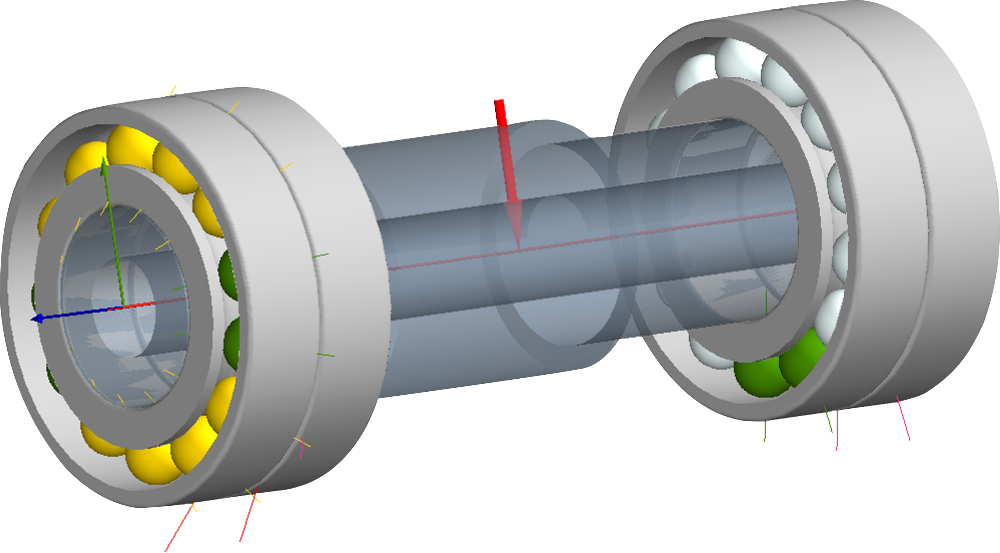Enerzijds lijkt het hiermee een eenvoudige formule, anderzijds liggen er aan de bepaling van de verschillende grootheden een heleboel gegevens ten grondslag. Zo is het dynamische draaggetal afhankelijk van de diameter en de lengte van de wentellichamen, het aantal wentellichamen, het aantal rijen en de contacthoek. Indien gewenst, is het draaggetal dus zelf te bepalen, maar in principe ook gewoon te vinden in de catalogus van de leverancier.
In de loop der jaren is de misvatting ontstaan dat een hoger dynamisch draaggetal automatisch leidt tot een hogere kwaliteit van het lager en hiermee een langere levensduur. In bepaalde gevallen is dit inderdaad waar, maar als de wentellichamen groter worden uitgevoerd in diameter, waardoor de afmetingen van de binnen- en buitenring afnemen, dan leidt dit onherroepelijk tot een minder sterk lager en hiermee juist een lágere levensduur.
Conclusie: lagers met een identiek dynamisch draaggetal hoeven in de praktijk niet dezelfde levensduur te hebben, wat het dus lastig maakt om een correcte vergelijking te maken tussen lagers van diverse leveranciers.
"Lagers met een identiek dynamisch draaggetal hoeven in de praktijk niet dezelfde levensduur te hebben, wat het dus lastig maakt om een correcte vergelijking te maken tussen lagers van diverse leveranciers"
Onderzoek
Hoe groot die verschillen dan wel kunnen zijn, blijkt uit een onderzoek van lagerfabrikant SKF, waarbij men de levensduur van lagers van diverse leveranciers met verschillende dynamische draaggetallen met elkaar vergelijkt. Concreet belichtte het onderzoek de levensduur van 35 lagers van iedere fabrikant van het lagertype 22220 met een asboring van 100 mm. Tijdens de test ging men de lagers radiaal belasten met 140 kN onder identieke smeercondities en bedrijfstemperatuur. De resultaten gaven ten eerste aan dat enkele lagers de theoretische levensduur van 25 miljoen omwentelingen niet eens haalden. Opmerkelijker was dat de beste lagers uitkwamen op een levensduur die tot zestien maal hoger lag dan de berekende waarde! Schijnbaar bleken de grootheden die tot dan toe werden meegenomen in de levensduurberekening, niet voldoende en speelden nog andere factoren een rol.
UITBREIDING FORMULE
Op zich waren de uitkomsten niet verrassend. Al veel langer was bekend dat niet uitsluitend de componenten van het lager zelf de levensduur bepalen, maar dat ook materialen, productietechnieken, verontreiniging en smering een significante invloed hebben. Door het vertalen van deze inzichten naar de oorspronkelijke formule is er door SKF-specialisten uiteindelijk een aparte factor toegevoegd waarin deze factoren zijn ondergebracht. Het gaat hierbij om de smeringscondities, uitgedrukt in de viscositeitsverhouding ĸ (kappa), de graad van verontreiniging ƞc en de verhouding tussen de belasting en vermoeiingsgrens Pu. Deze drie factoren worden samengebracht in 'askf', een factor die uiteindelijk via een tabel kan worden afgelezen of wordt meegenomen in moderne software voor het berekenen van de levensduur van lagers.
Elementen van de nieuwe factor
De nieuwe formule laat onder andere zien hoe belangrijk goede smering is voor de levensduur van een lager. Dit heeft vooral te maken met het feit dat een goede smering veranderingen áán het oppervlak - zoals in het begin van de tekst is toegelicht - kan voorkomen.
De kwaliteit van de smeerfilm is daarbij te beschrijven middels de kappa-waarde; dit is de verhouding tussen de bedrijfsviscositeit van het smeermiddel en de nominale viscositeit, afhankelijk van de diameter van het lager en het toerental.
De formule van deze viscositeitsverhouding ĸ - Kappa - is hieronder weergegeven en geeft onder meer aan dat een volledige smering bijdraagt aan een veel langere levensduur dan een grenssmering waarbij de waarde van ĸ onder de 1 ligt.
De verontreiniging in het lager is een ervaringsgetal dat kan worden bepaald door bijvoorbeeld het nemen van oliemonsters. Deze factor wordt uitgedrukt in ƞc. De volgende nieuweling in de formule - de belasting van het lager - is uiteraard afhankelijk van de applicatie, terwijl de vermoeiingsgrens te selecteren is uit de documentatie van de fabrikant.
Aflezen uit de grafiek
Na het berekenen, opzoeken en bepalen van de viscositeitsverhouding, de vervuilingsfactor, de belasting en de vermoeiingsgrens is de bijbehorende askf-factor af te lezen uit een tabel zoals onderstaande. Als voorbeeld nemen we een ƞc * Pu/P = 1 en een ĸ‑waarde van 0,7 (een relatief slechte smering dus). Door op de x-as vanaf 1 naar boven te gaan tot de ĸ‑waarde 0,7, is vervolgens op de y-as af te lezen dat de askf-factor 27 bedraagt. Dit betekent een levensduur die 27 keer hoger ligt dan de levensduur zoals deze bepaald zou zijn met de 'oude' rekenmethode. Ga je naar een ĸ‑waarde van 1 of hoger, dan loopt de askf-factor nog vele malen hoger op.
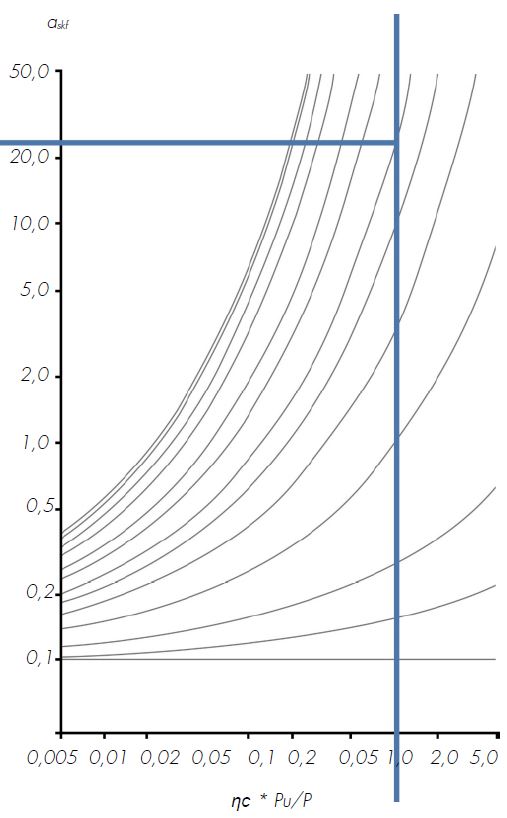
CONCLUSIE
Hoewel de nieuwe formule feitelijk al tien jaar bekend is, zijn er nog steeds te veel engineers en constructeurs die gewoontegetrouw gebruikmaken van de oude formule. Een gemiste kans. Door factoren als 'smering' mee te nemen, zullen berekeningen uitwijzen dat er waarschijnlijk een lichter - en goedkoper - lager kan worden toegepast. Het toepassen van de verbeterde formule voorkomt zo overdimensionering en bespaart kosten met behoud van de betrouwbaarheid en kwaliteit van de installaties. Bovendien wordt de toepassing van de formule ook ondersteund door moderne lagerberekeningssoftware die automatisch vraagt om de bijbehorende gegevens. Zeker bij online beschikbare programma's heeft de gebruiker daarbij het voordeel dat hij steeds gebruikmaakt van de meest recente informatie ten aanzien van onder andere de eigenschappen van smeermiddelen en (nieuwe) materialen. Een kleine moeite om problemen te kunnen vermijden!
